dlmtree

dlmtree is an R package that provides constrained distributed lag models (DLMs) using a regression tree approach within the Bayesian additive regression trees (BART) framework, referred to as treed DLMs. The package includes various extensions of treed DLMs, allowing for the incorporation of different scenarios like linear, non-linear associations, mixture exposures, and heterogeneous exposure effects. The package is built user-friendly with a single function with three arguments to specify treed DLMs. Functions for summarizing the model fit and visualization are also provided.

Treed DLM Overview

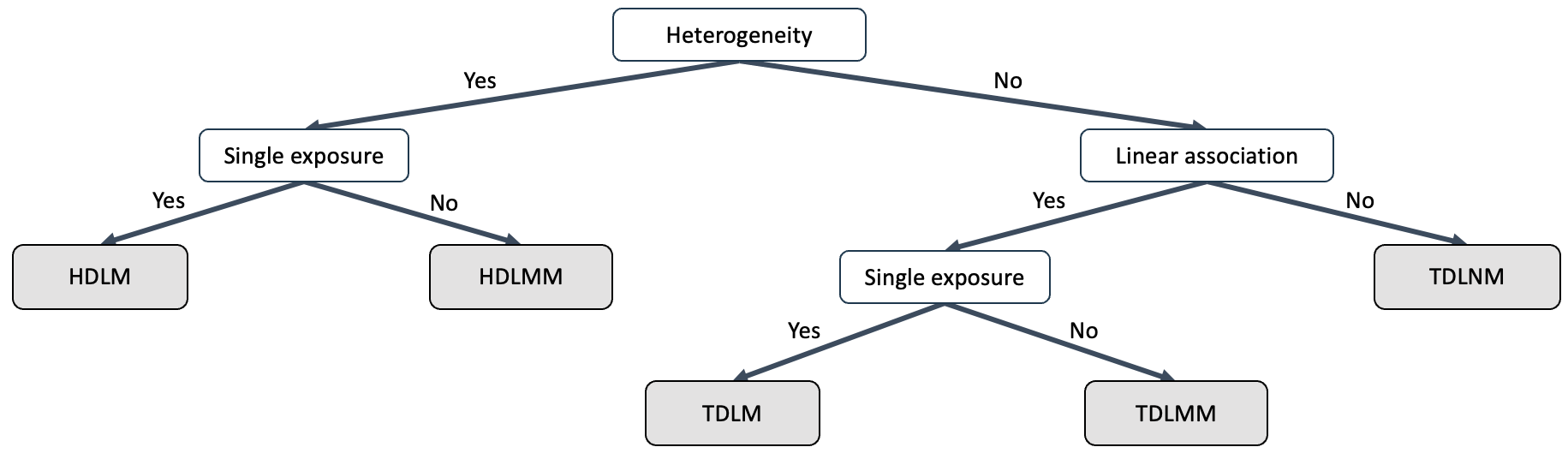
Model Type Family Mixture Heterogeneity
Treed distributed lag model (TDLM)\(^2\) Linear Gaussian X X
Binary X X
Count X X
Treed distributed lag mixture model (TDLMM)\(^2\) Linear Gaussian O X
Binary O X
Count O X
Treed distributed non-linear lag model (TDLNM)\(^{1,4}\) Non-linear Gaussian X X
Binary X X
Monotone Gaussian X X
Binary X X
Heterogeneous distributed lag model (HDLM)\(^3\) Linear Gaussian X O
Heterogeneous distributed lag mixture model (HDLMM) Linear Gaussian O O

Model Selection Guide

Installation

Installing package from GitHub:

# install.packages("devtools")
devtools::install_github("danielmork/dlmtree")
library(dlmtree)

Installing package from CRAN:

install.packages("dlmtree")
library(dlmtree)

References

The majority of methods implemented in this package are described in the following papers as well as some on going work.

  1. Mork, D. and Wilson, A. (2022). “Treed distributed lag nonlinear models.” Biostatistics, 23(3), 754–771 (DOI: 10.1093/biostatistics/kxaa051, arXiv preprint)

  2. Mork, D. and Wilson, A. (2023). “Estimating perinatal critical windows of susceptibility to environmental mixtures via structured Bayesian regression tree pairs.” Biometrics, 79(1), 449-461 (DOI: 10.1111/biom.13568, arXiv preprint)

  3. Mork, D., Kioumourtzoglou, M. A., Weisskopf, M., Coull, B. A., and Wilson, A. (2024). “Heterogeneous Distributed Lag Models to Estimate Personalized Effects of Maternal Exposures to Air Pollution.” Journal of the American Statistical Association, 119(545), 14-26 (DOI: 10.1080/01621459.2023.2258595, arXiv preprint)

  4. Mork, D. and Wilson, A. (In press). “Incorporating prior information into distributed lag nonlinear models with zero-inflated monotone regression trees.” Bayesian Analysis. (DOI: 10.1214/23-BA1412, arXiv preprint)