pedprobr

Introduction

The main content of pedprobr is an implementation of the Elston-Stewart algorithm for pedigree likelihoods given marker genotypes. It is part of the pedsuite, a collection of packages for pedigree analysis in R.

The pedprobr package does much of the hard work in several other pedsuite packages:

• forrel : relatedness analysis and forensic pedigree analysis
• dvir : disaster victim identification
• paramlink2 : parametric linkage analysis
• pedbuildr : pedigree reconstruction

The workhorse of pedprobr is the likelihood() function, supporting a variety of situations:

• autosomal and X-linked markers
• a single marker or two linked markers
• complex inbred pedigrees
• pedigrees with inbred founders
• mutation models

Installation

To get the current official version of pedprobr, install from CRAN as follows:

install.packages("pedprobr")

Alternatively, you can obtain the latest development version from GitHub:

# install.packages("devtools") # install devtools if needed
devtools::install_github("magnusdv/pedprobr")

Getting started

library(pedprobr)
#> Loading required package: pedtools

To set up a simple example, we first use pedtools utilities to create a pedigree where two brothers are genotyped with a single SNP marker. The marker has alleles a and b, with frequencies 0.2 and 0.8 respectively, and both brothers are heterozygous a/b.

# Pedigree with SNP marker
x = nuclearPed(nch = 2) |> 
  addMarker(geno = c(NA, NA, "a/b", "a/b"), afreq = c(a = 0.2, b = 0.8))

# Plot with genotypes
plot(x, marker = 1)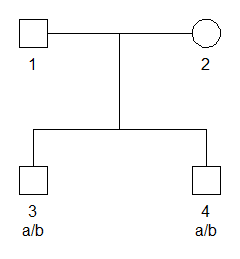

The pedigree likelihood, i.e., the probability of the genotypes given the pedigree, is obtained as follows:

likelihood(x, marker = 1)
#> [1] 0.1856

Genotype probability distributions

Besides likelihood(), other important functions in pedprobr are:

• oneMarkerDistribution() : the joint genotype distribution at a single marker, for any subset of pedigree members
• twoMarkerDistribution() : the joint genotype distribution at two linked markers, for a single person

In both cases, the distributions are computed conditionally on any known genotypes at the markers in question.

To illustrate oneMarkerDistribution() we continue our example from above, and consider the following question: What is the joint genotype distribution of the parents, conditional on the genotypes of the children?

The answer is found as follows:

oneMarkerDistribution(x, ids = 1:2, partialmarker = 1, verbose = F)
#>            a/a        a/b       b/b
#> a/a 0.00000000 0.01724138 0.1379310
#> a/b 0.01724138 0.13793103 0.2758621
#> b/b 0.13793103 0.27586207 0.0000000

The output confirms the intuitive result that the parents cannot both be homozygous for the same allele. The most likely combination is that one parent is heterozygous a/b, while the other is homozygous b/b.